Overview

In this lab you will learn how to locate elements of symmetry in molecules and how to demonstrate the results of symmetry operations.

1) Make following molecules (H₂O, BF₃, CH₄, PCl₅, C₂H₆, SF₆)using balls and sticks given.

Draw them below:
 
 
 
 
 
 
 
 
 
 

Background

Molecular symmetry is of great value in understanding molecular bonding and spectroscopy. The symmetry of a molecule is expressed as a collection of symmetry operations or elements of symmetry. A molecule with a particular set of symmetry elements is said to belong to a particular point group. Molecular orbitals and vibrations within molecules also have symmetry properties. Symmetry operations are manipulations of a molecule which result in indistinguishable representations of the molecule; that is, a molecule looks no different before and following a symmetry operation. The operation may exchange two identical atoms, or it may leave one or more atoms unmoved.

The symmetry operations are as follows:

Identity (E): The identity is a trivial symmetry operation which involves doing nothing to the molecule. It is mentioned here only for the sake of completeness. All molecules possess an identity and, in some molecules, the identity is the only element of symmetry.

2) Write how identity (E) is obtained for BF₃, CH₄, PCl₅, C₂H₆, SF₆ .
 
 
 
 
 
 
 
 

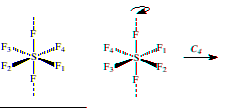
Axis of Rotation (C_n): An n-fold axis of rotation is a rotation about an axis by 360°/n. Often, but not always, rotation axes correspond to bond axes. For example, SF₆ possesses a C₄ axis which passes through opposing S-F bonds. Rotation by 90° about the axis rotates each fluorine atom perpendicular to the axis into a position previously occupied by another fluorine atom.

3) Draw a model depicting C₄ axises of SF₆.

SF₆ also possesses 3 C₃ axes of rotation which do not pass through bonds. In the following representation, the C₃ axis is perpendicular to the plane of the paper and passes through the sulfur atom.

4) Draw a model depicting C₃ axises of SF₆.

Rotate a molecule

1. Center the molecule in the window by selecting the entire molecule and pressing f on the keyboard. It may resize the molecule in the process of centering it. If the molecule is not centered in the window, it will wobble as the rotation commands are executed.
2. Rotate the molecule until the rotation axis is perpendicular to the screen. You should now be looking directly down the rotation axis, which should be centered in the window.
3. Press r on the keyboard to enter rotation mode.
4. Press z to rotate in the clockwise direction and Z to rotate counter-clockwise. Rotate around the x and y axes by pressing x, X, y or Y. Rotation occurs by 15° each time. Thus three operations result in a 45°rotation, 4 - 60°, 6 - 90°, 8 -120°, etc. You may rotate continuously by pressing the Space bar while in rotate mode. To halt continuous rotation, press the Space bar again.

5) Make a drawing of your model depicting mirror planes.

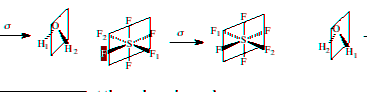
Reflect through a mirror plane

Improper Rotation or rotation-reflection (S_n): An improper rotation is the result of two operations in sequence; rotation by 360°/n, followed by reflection through a mirror plane perpendicular to the axis of rotation. An example of an improper axis of rotation is shown below.

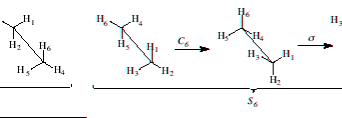
Execute and demonstrate an improper rotation

Follow the procedures for rotation and reflection in sequence.

6) To demonstrate the example above, label carbon and hydrogen atoms, write the operations for each step

7) Label carbon and hydrogen atoms and write two operations (C₃ and s) of on the diagram below

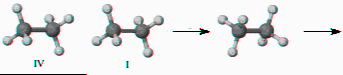
Inversion (i): An inversion through the center of a molecule can usually be accomplished by a rotation by 180° followed by reflection through a plane (Mirror operation) perpendicular to the rotation. Note that this is identical to an S₂ as in the example below (rotation by 180° about the C-C axis followed by reflection through a plane perpendicular to the C-C axis).

8) Label carbon and hydrogen atoms and write operation (i) of on the diagram below

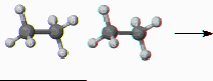
A planar molecule, an inversion is simply accomplished via rotation by 180° about an axis perpendicular to the plane since subsequent reflection through the plane leaves the molecule unchanged.

8) Label boron and fluorine atoms in BF₃ and write operation (i) of on a diagram.

Point Groups

Two molecules are in the same point group if they possess the same elements of symmetry. The first step in a group theory analysis of a molecule is to determine the point group of the molecule. There is a systematic way of naming most point groups

9) Using the chart given blow assign the point group to each of the following molecules

1. H₂O

 

 
 
 

2. BF₃

 

 
 
 

3. CH₄

 

 
 
 

4. PCl₅

1. C₂H₆

 

 
 
 

2. SF₆)

The top row and first column consist of the symmetry operations and irreducible representations respectively. The table elements are the characters. The final two columns show the first and second order combinations of Cartesian coordinates. Infinitesimal rotations are listed as I_x, I_y, and I_z.

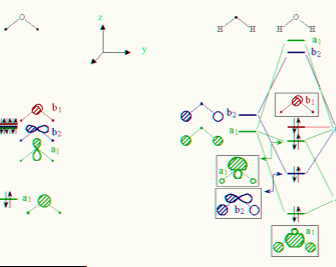
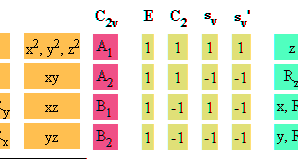
Character table for point group C_2v, H₂O, water molecule

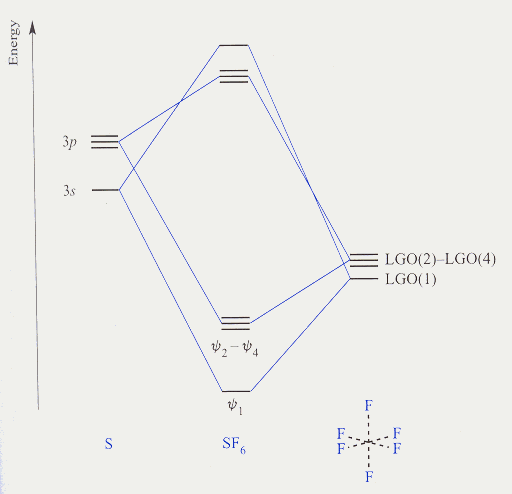
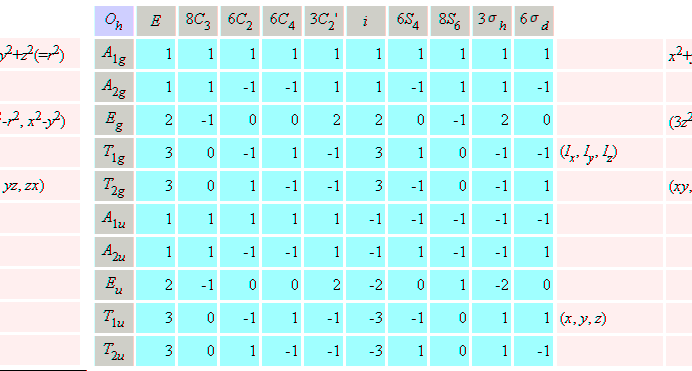
Character table for point group O_h, SF₆,

10)

a) Using character table for point group C_2v, H₂O, water molecule identify symmetry representation of s, p_x, p_y and p_x atomic orbitals on oxygen atom of water molecule.
 
 
 
 

b) Using character table for point group O_h, SF₆, s, p_x, p_y p_x, d_z2, d_x2-y2, d_xy, and d_xz, d_yz atomic orbitals on sulfur atom of SF₆ molecule.
 
 
 
 

11) Comment on the symmetries of the molecular orbital diagrams of H₂O and SF₆