Powder X-Ray Diffraction (PXRD)What is X-ray Crystallography ?

X-ray crystallography is an experimental technique that exploits the fact that X-rays are
diffracted by crystals. It is not an imaging technique. X-rays have the proper wavelength (in the Ångström range, ~10-8 cm) to be scattered by the electron cloud of an atom of comparable size. Based on the diffraction pattern obtained from X-ray scattering off the periodic assembly of
molecules or atoms in the crystal, the electron density can be reconstructed. Additional phase information must be extracted either from the diffraction data or from supplementing diffraction experiments to complete the reconstruction (the phase problem in crystallography). A
model is then progressively built into the experimental electron density, refined against the data and the result is a quite accurate molecular structure.

Miller Indices

Rules for Miller Indices:

Determine the intercepts of the face along the crystallographic axes, in terms of unit cell dimensions.
Take the reciprocals
Clear fractions
Reduce to lowest terms

For example, if the x-, y-, and z- intercepts are 2, 1, and 3, the Miller indices are calculated as:

Take reciprocals: 1/2, 1/1, 1/3
Clear fractions (multiply by 6): 3, 6, 2
Reduce to lowest terms (already there)

Thus, the Miller indices are 3,6,2. If a plane is parallel to an axis, its intercept is at infinity and its Miller index is zero. A generic Miller index is denoted by (hkl).

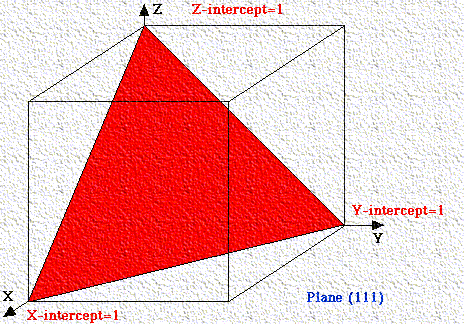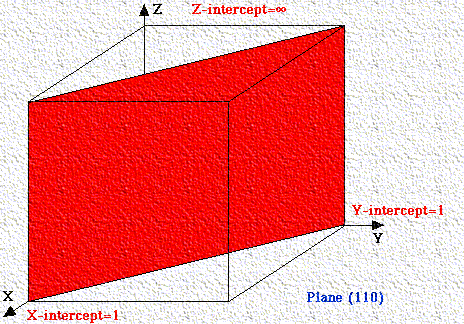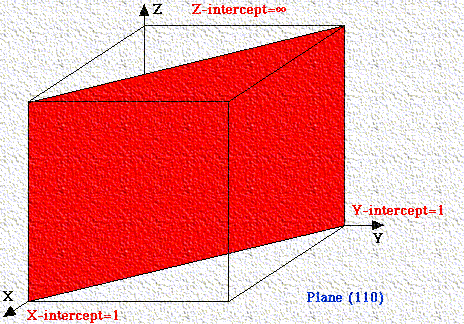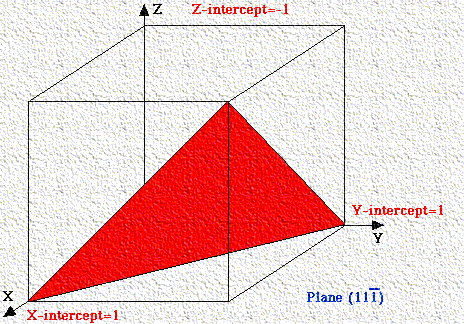
If a plane has negative intercept, the negative number is denoted by a bar above the number. Never alter negative numbers. For example, do not divide -1, -1, -1 by -1 to get 1,1,1. This implies symmetry that the crystal may not have!

Some General Principles

If a Miller index is zero, the plane is parallel to that axis.
The smaller a Miller index, the more nearly parallel the plane is to the axis.
The larger a Miller index, the more nearly perpendicular a plane is to that axis.
Multiplying or dividing a Miller index by a constant has no effect on the orientation of the plane
Miller indices are almost always small.

Bragg's Law and Diffraction:
Bragg's Law refers to the simple equation:

nl = 2d sinq (1)

derived by the English physicists Sir W.H. Bragg and his son Sir W.L. Bragg in 1913 to explain why the cleavage faces of crystals appear to reflect X-ray beams at certain angles of incidence (theta, q). The variable d is the distance between atomic layers in a crystal, and the variable lambda l is the wavelength of the incident X-ray beam (see applet); n is an integer

This observation is an example of X-ray wave interference (Roentgenstrahlinterferenzen), commonly known as X-ray diffraction (XRD), and was direct evidence for the periodic atomic structure of crystals postulated for several centuries. The Braggs were awarded the Nobel Prize in physics in 1915 for their work in determining crystal structures beginning with NaCl, ZnS and diamond. Although Bragg's law was used to explain the interference pattern of X-rays scattered by crystals, diffraction has been developed to study the structure of all states of matter with any beam, e.g., ions, electrons, neutrons, and protons, with a wavelength similar to the distance between the atomic or molecular structures of interest.

Bragg's Law can easily be derived by considering the conditions necessary to make the phases of the beams coincide when the incident angle equals and reflecting angle. The rays of the incident beam are always in phase and parallel up to the point at which the top beam strikes the top layer at atom z (Fig. 1). The second beam continues to the next layer where it is scattered by atom B. The second beam must travel the extra distance AB + BC if the two beams are to continue traveling adjacent and parallel. This extra distance must be an integral (n) multiple of the wavelength (l) for the phases of the two beams to be the same:

nl = AB +BC (2).

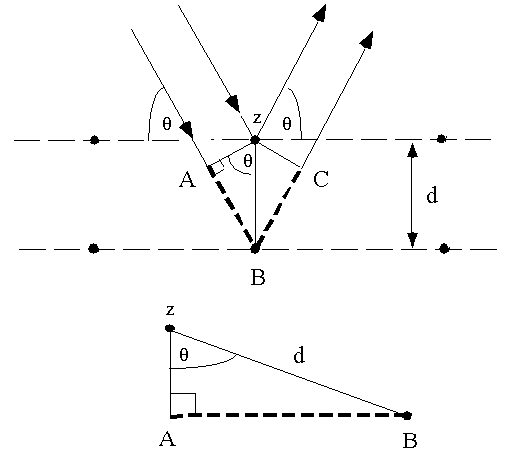
Fig. 1 Deriving Bragg's Law using the reflection geometry and applying trigonometry. The lower beam must travel the extra distance (AB + BC) to continue traveling parallel and adjacent to the top beam.

Recognizing d as the hypotenuse of the right triangle Abz, we can use trigonometry to relate d and q to the distance (AB + BC). The distance AB is opposite q so,

AB = d sinq (3).

Because AB = BC eq. (2) becomes,

nl = 2AB (4)

Substituting eq. (3) in eq. (4) we have,

nl = 2 d sinq, (1)

and Bragg's Law has been derived. The location of the surface does not change the derivation of Bragg's Law.

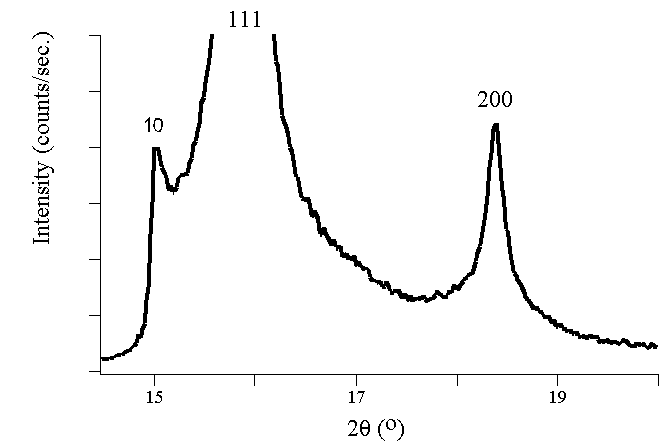
Experimental Diffraction Patterns

The following figures show experimental x-ray diffraction patterns of cubic SiC using synchrotron radiation.

Players in the Discovery of X-ray Diffraction

Friedrich and Knipping first observed Roentgenstrahlinterferenzen in 1912 after a hint from their research advisor, Max von Laue, at the University of Munich. Bragg's Law greatly simplified von Laue's description of X-ray interference. The Braggs used crystals in the reflection geometry to analyze the intensity and wavelengths of X-rays (spectra) generated by different materials. Their apparatus for characterizing X-ray spectra was the Bragg spectrometer.

Laue knew that X-rays had wavelengths on the order of 1 Å. After learning that Paul Ewald's optical theories had approximated the distance between atoms in a crystal by the same length, Laue postulated that X-rays would diffract, by analogy to the diffraction of light from small periodic scratches drawn on a solid surface (an optical diffraction grating). In 1918 Ewald constructed a theory, in a form similar to his optical theory, quantitatively explaining the fundamental physical interactions associated with XRD. Elements of Ewald's eloquent theory continue to be useful for many applications in physics.